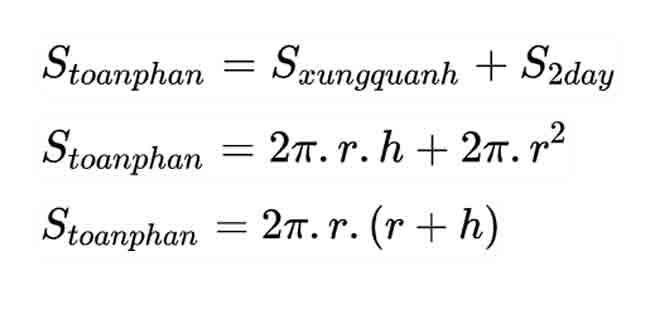
Phương trình tính diện tích bề mặt xung quanh
– Khái niệm
Diện tích bề mặt xung quanh hình trụ tròn chỉ gồm diện tích mặt xung quanh, bao quanh hình trụ tròn và không bao gồm diện tích hai đáy.
Hình trụ thường được đề cập với hai khái niệm: bề mặt xung quanh và toàn bộ.
Bạn đang xem: ✅ Công thức tính diện tích xung quanh hình trụ ⭐️⭐️⭐️⭐️⭐
- Bề mặt xung quanh của hình trụ chỉ bao gồm diện tích mặt xung quanh, bao quanh hình trụ và không bao gồm diện tích hai đáy.
- Toàn bộ bề mặt được tính là tổng diện tích của toàn bộ không gian mà hình trụ chiếm, bao gồm cả diện tích bề mặt xung quanh và diện tích hai đáy tròn.
– Phương trình
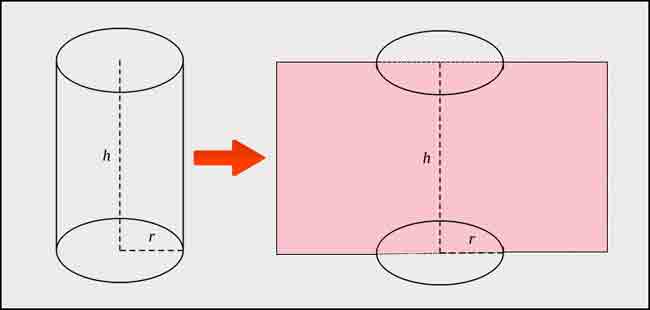
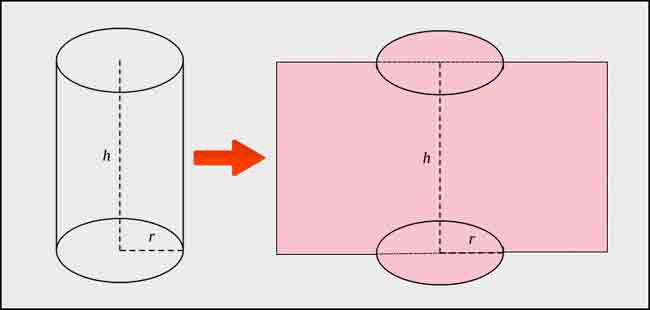
Phương trình tính diện tích bề mặt xung quanh là chu vi của đường tròn đáy nhân với chiều cao.
Sxq = 2.π.r.h
Xem thêm : Công thức thấu kính
Trong đó:
– r: Bán kính hình trụ.
– h: Chiều cao từ đáy đến đỉnh của hình trụ.
Xem thêm : ✅ Công thức who whom which ⭐️⭐️⭐️⭐️⭐
– π = 3.14159265359
– Ví dụ
Một hình trụ tròn có bán kính đáy r = 5 cm, chiều cao h = 7cm. Hãy tính diện tích bề mặt xung quanh của hình trụ đứng.
Hướng dẫn giải: Diện tích bề mặt xung quanh của hình trụ tròn: Sxq = 2.π.r.h = 2π.5.7 = 70π = 219,8 (cm2).
Ví dụ 1: Một bóng đèn huỳnh quang dài 1,2m, đường kính của đường tròn đáy là 4cm, được đặt khít vào một ống giấy cứng dạng hình hộp (h.82). Tính diện tích phần giấy cứng dùng để làm một hộp.
Lời giải:
Diện tích phần giấy cứng cần tính chính là diện tích bề mặt xung quanh của một hình hộp có đáy là hình vuông cạnh 4cm, chiều cao 1,2m = 120cm.
Diện tích bề mặt xung quanh của hình hộp là tổng diện tích của bốn hình chữ nhật bằng nhau với chiều dài là 120 cm và chiều rộng 4cm:
Sxq= 4.4.120 = 1920 cm2
Ví dụ 2: Mô hình của một cái lọ thí nghiệm dạng hình trụ (không nắp) có bán kính đường tròn đáy 14cm,chiều cao 10cm. Tìm diện tích bề mặt xung quanh cộng với diện tích một đáy
Lời giải:

Phương trình tính diện tích toàn bộ
– Giới thiệu
Diện tích toàn bộ là tổng diện tích của toàn bộ không gian mà hình trụ chiếm, bao gồm cả diện tích bề mặt xung quanh và diện tích hai đáy tròn.
– Phương trình
Phương trình tính diện tích 2 đáy tròn đáy
S2đ=2πr2(Sđ=πr2)
Phương trình tính diện tích toàn bộ bằng diện tích bề mặt xung quanh cộng với diện tích của 2 đáy.
Stp = Sxq + 2.Sđáy = 2.π.r2 + 2.π.r.h
Xem thêm : Công thức thấu kính
Trong đó:
– r: Bán kính hình trụ.
– h: Chiều cao hình trụ.
Xem thêm : ✅ Công thức who whom which ⭐️⭐️⭐️⭐️⭐
– π = 3.14159265359
– Ví dụ
Một hình trụ tròn có bán kính đáy r = 4 cm, chiều cao h = 6 cm. Hãy tính diện tích toàn bộ của hình trụ đứng.
Hướng dẫn giải: Stp = Sxq + 2.Sđáy= 2.π.r2 + 2.π.r.h = 2.π.42 + 2.π.4.6 = 32π + 48π = 80π (cm2).
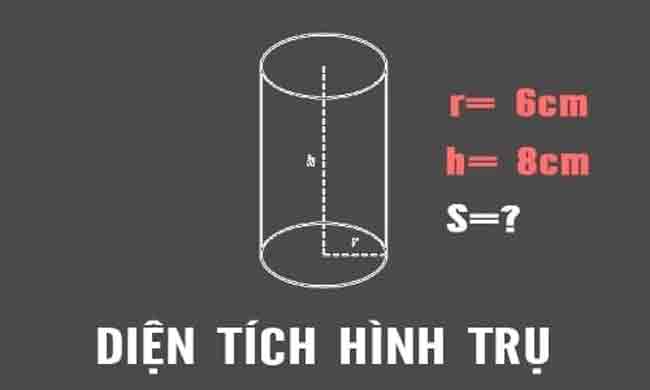
Ví Dụ Cách Tính Diện Tích Hình Trụ:
Cho một hình trụ có bán kính đường tròn đáy là 6 cm , trong khi đó chiều cao từ đáy đến đỉnh của hình trụ là 8 cm. Hỏi diện tích bề mặt xung quanh và diện tích toàn bộ của hình trụ là bao nhiêu?
Theo công thức ta có bán đường tròn đáy r = 6 cm và chiều cao của hình trụ h = 8 cm . Suy ra ta có công thức tính diện tích bề mặt xung quanh và diện tích toàn bộ của hình trụ như sau:
– Diện tích bề mặt xung quanh hình trụ = 2 x π x r x h = 2 x π x 6 x 8 = ~ 301 cm2
– Diện tích toàn bộ hình trụ = 2 x π x r2 x (r + h) = 2 x π x 6 x (6 + 8) = ~ 527 cm2.
Ví dụ
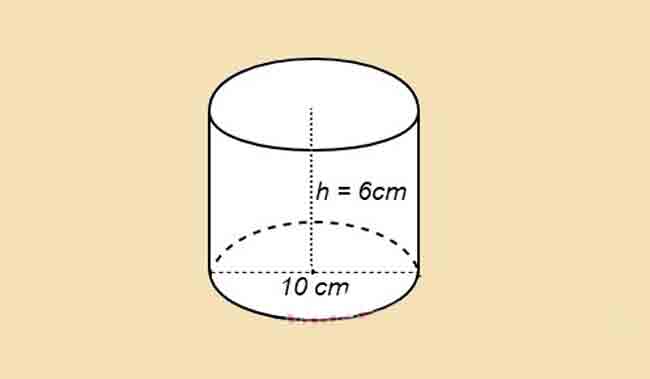
Ví dụ 1: Tính diện tích toàn bộ của hình trụ, có độ dài đường tròn đáy là 10cm, khoảng cách giữa 2 đáy là 6cm.
Giải
Theo đề bài ta có: h = 6cm; 2r = 10cm => r = 5cm.
Áp dụng công thức tính diện tích toàn bộ hình trụ:
Stp=2πr(r+h)=2π.5(5+6)=110π(cm2)
=> Vậy diện tích toàn bộ của hình trụ là 110π(cm2)
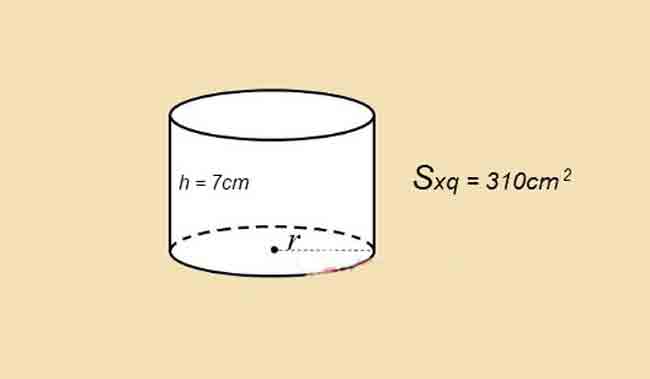
Ví dụ 2: Tính diện tích toàn bộ của hình trụ có chiều cao là 7cm và diện tích bề mặt xung quanh là 310 (cm2)
Giải
Theo đề bài ta có: h = 7; Sxq=310
Áp dụng công thức tính diện tích bề mặt xung quanh: Sxq=2πrh
=> r=Sxq2πrh=3102π.7≈7cm
Vậy Sđ=πr2=π.72=49π≈154cm2
=> Diện tích toàn bộ của hình trụ: Stp=2.Sđ+Sxq=2.154+310=618cm2
Phương trình tính thể tích hình trụ tròn
– Giới thiệu
Thể tích hình trụ tròn là khoảng không gian mà nó chiếm.
– Phương trình
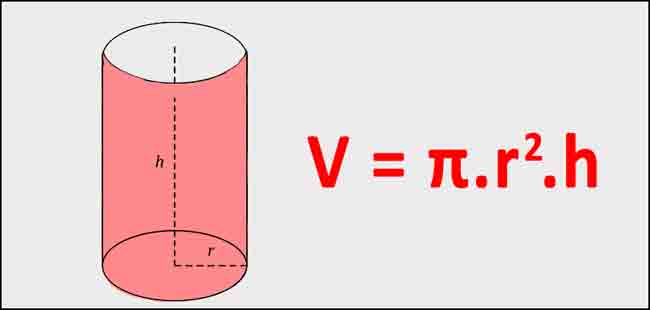
Phương trình tính thể tích hình trụ tròn bằng diện tích của mặt đáy nhân với chiều cao.
V = π.r2.h.
Xem thêm : Công thức thấu kính
Trong đó:
– r: Bán kính hình trụ.
– h: Chiều cao từ đáy đến đỉnh của hình trụ.
Xem thêm : ✅ Công thức who whom which ⭐️⭐️⭐️⭐️⭐
– π = 3.14159265359
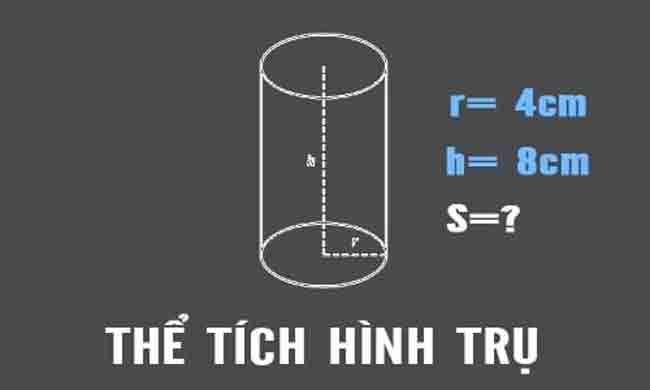
– Ví dụ
Một hình trụ tròn có bán kính đáy r = 8 cm, chiều cao h = 6 cm. Hãy tính diện tích bề mặt xung quanh, diện tích toàn bộ và thể tích của hình trụ.
Hướng dẫn giải: Thể tích khối trụ: V = π.r2.h = π.64.6 = 384π (cm3).
– Ví Dụ Cách Tính Diện Tích Hình Trụ:
Cho một hình trụ có bán kính đường tròn đáy là 6 cm , trong khi đó chiều cao từ đáy đến đỉnh của hình trụ là 8 cm. Hỏi thể tích của hình trụ là bao nhiêu?
Theo đó, ta áp dụng vào phương trình tính thể tích hình trụ và có: bán kính đường tròn đáy hình trụ r = 6cm và chiều cao hình trụ h = 8cm. Suy ra, ta có công thức tính thể tích hình trụ như sau:
V = π x r2 x h = π x 62 x 8 = ~ 402 cm3
Ví dụ 2: Tính thể tích của một hình trụ có đường kính đáy là 10cm, và khoảng cách giữa hai đáy là 6cm.
Giải
Theo đề bài ta có: r = 5cm; h = 6cm.
Áp dụng công thức tính thể tích hình trụ:
Vp=πr2h=π.52.6=150π(cm3)
=> Vậy thể tích của hình trụ là 150π(cm3)
Ví dụ 3: Tính thể tích của một hình trụ biết diện tích mặt xung quanh của nó là 500 (cm2), biết bán kính đáy của hình trụ là 5cm.

Lời giải:
Theo đề bài ta có: r = 5; Sxq=500
Áp dụng công thức tính diện tích bề mặt xung quanh: Sxq=2πrh
=> h=Sxq2πrh=5002π.5≈15cm
Thể tích của hình trụ: V=πr2h=π.52.15≈375π(cm3)
Định nghĩa về hình trụ
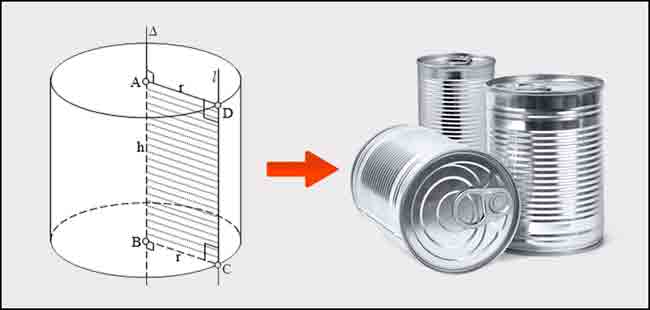
Hình trụ là một hình học được bao quanh bởi hai đường tròn có đường kính bằng nhau và một mặt trụ.
Hình trụ tròn là hình trụ được tạo ra bằng việc xoay một hình chữ nhật xung quanh trục cố định, hai đáy của nó là hai hình tròn bằng nhau và song song với nhau.
Hình trụ tròn là loại hình trụ có hai đáy là hai hình tròn bằng nhau và song song với nhau. Hình trụ được sử dụng rộng rãi trong các bài toán hình học từ cơ bản đến phức tạp, trong đó công thức tính diện tích và thể tích hình trụ được sử dụng hàng ngày. Nếu bạn đã biết cách tính diện tích và chu vi hình tròn thì cũng có thể dễ dàng áp dụng để tính toán diện tích bề mặt xung quanh, diện tích toàn bộ và thể tích của hình trụ.
Nguồn: https://vatlytuoitre.com
Danh mục: Định luật
