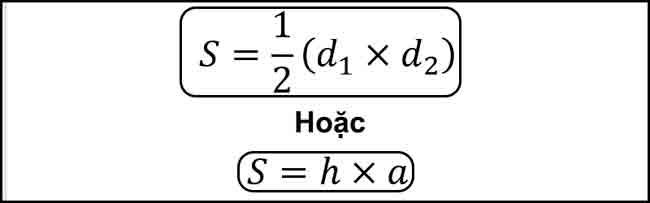
Công thức tính diện tích hình thoi, chu vi hình thoi đầy đủ nhất
1. Công thức tính diện tích hình thoi
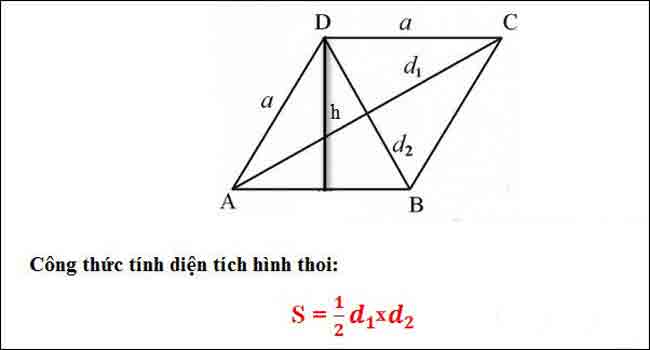
Công thức tính dựa đường chéo
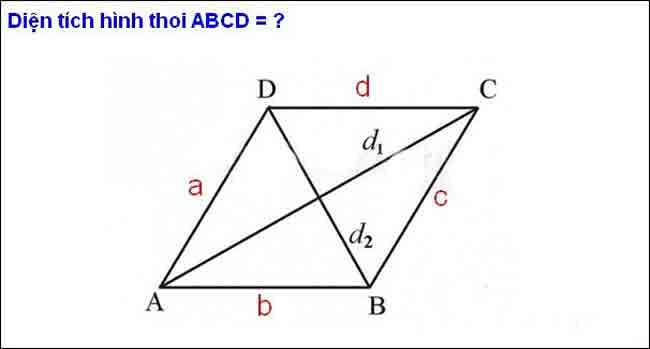
Trong công thức diện tích hình thoi, chúng ta có các biến sau:
+ d1: đường chéo thứ nhất
Bạn đang xem: ✅ Công thức tính diện tích hình thoi ⭐️⭐️⭐️⭐️⭐
+ d2: đường chéo thứ hai
Ví dụ: Có một tấm bìa hình thoi đo được hai đường chéo tạo thành góc với độ dài lần lượt là 6 cm và 8 cm. Hỏi diện tích của tấm bìa hình thoi đó bằng bao nhiêu?
Áp dụng công thức tính diện tích hình thoi, ta có d1 = 6 cm và d2 = 8 cm. Ta đưa vào công thức và có kết quả như sau:
S = 1/2 x (d1 x d2) = 1/2 (6 x 8) = 1/2 x 48 = 24 cm2
Ví dụ 1 : Tính diện tích hình thoi có các đường chéo bằng 6cm và 8cm.
Lời giải Ta có: Độ dài 2 đường chéo có ở đề bài lần lượt là 6 và 8. Diện tích hình thoi là: 1/2.(6 × 8)= 24 cm2 Do đó, diện tích của một hình thoi là 24cm2 .
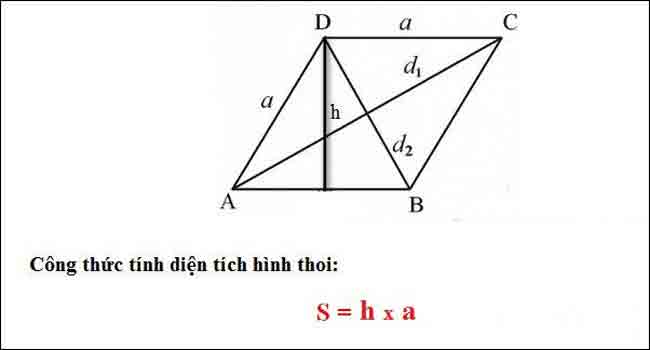
* Công thức tính diện tích hình thoi dựa vào cạnh đáy và chiều cao
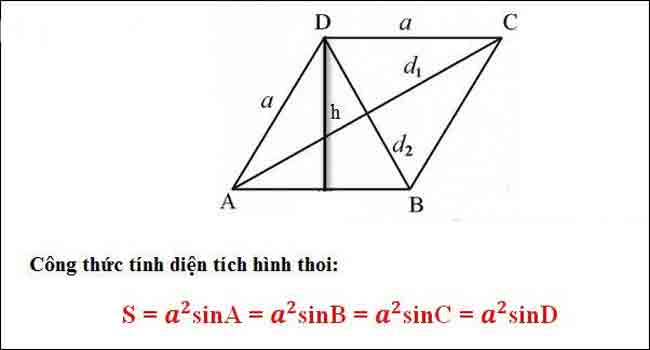
Trong công thức diện tích hình thoi, chúng ta có các biến sau:
– h: Chiều cao của hình thoi
– a: Cạnh đáy
Ví dụ: Cho hình thoi ABCD, có cạnh AB = BC = CD = DA = 4 cm, chiều cao hình thoi bằng 3cm.
Giải: Áp dụng công thức diện tích hình thoi, ta có h = 3cm, a = 4cm. Ta thay vào công thức và có kết quả như sau:
S = a x h = 3 x 4 = 12 cm2
Ví dụ 2: Tính diện tích của hình thoi biết cạnh đáy của nó là 10 cm và chiều cao là 7 cm.
Lời giải: Ta có cạnh đáy a = 10 cm Chiều cao h = 7 cm Diện tích hình thoi là: S = a.h = 10 x 7 = 70 cm2
Công thức tính diện tích hình thoi dựa vào hệ thức trong tam giác (Nếu biết góc của hình thoi)
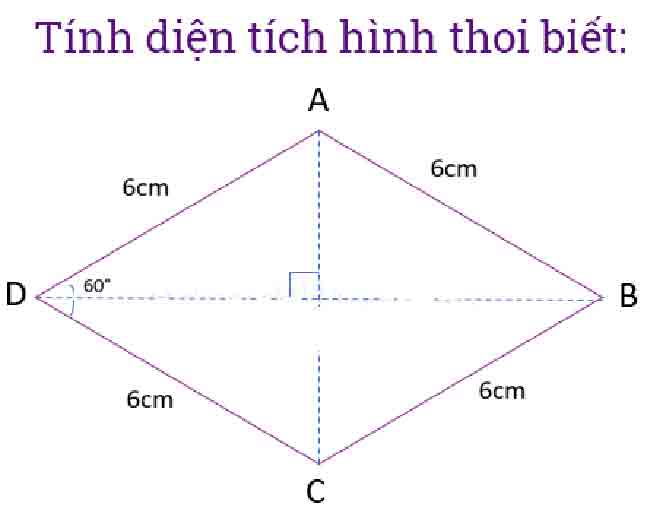
Trong công thức diện tích hình thoi, chúng ta có biến sau:
a: cạnh hình thoi
Ví dụ: Cho hình thoi ABCD, có cạnh hình thoi = 4cm, góc A = 35 độ. Tính diện tích hình thoi ABCD.
Lời giải
Xem thêm : ✅ Công thức Hóa Học lớp 12 ⭐️⭐️⭐️⭐️⭐
Áp dụng công thức, ta có a = 4, góc = 35 độ. Ta thay vào công thức như sau:
S = a2 x sinA = 42 x sin(35) = 9,176 (cm2)
Lưu ý:– Đơn vị diện tích của hình thoi là cm2
2. Tính chất và dấu hiệu nhận biết hình thoi
– Tính chất
+ Hình thoi có đầy đủ tính chất của hình bình hành. Đó là: Các cạnh đối song song và bằng nhau, các góc đối bằng nhau, hai đường chéo cắt nhau tại trung điểm mỗi đường.
+ Hai đường chéo của hình thoi vuông góc với nhau.
+ Hai đường chéo là các đường phân giác của các góc thuộc hình thoi.
– Dấu hiệu nhận biết
Để nhận biết được hình thoi bạn cần xem xét các điều kiện sau:
+ Tứ giác có 4 cạnh bằng nhau.
+ Hình bình hành có 2 cạnh liền kề bằng nhau.
+ Hình bình hành có 2 đường chéo vuông góc với nhau.
+ Hình bình hành có 1 đường chéo là đường phân giác của một góc.
3. Công thức tính chu vi hình thoi
– Công thức
Chu vi hình thoi bằng tổng độ dài các cạnh
C = a x 4.
– Trong đó:
+ C: Chu vi hình thoi.
+ a: Độ dài cạnh bất kỳ của hình thoi.
4. Phương pháp nhớ công thức tính chu vi, diện tích hình thoi
Hình thoi có công thức tính diện tích đơn giản và dễ nhớ, chỉ cần biết đường chéo hoặc cạnh của hình thoi là có thể tính được diện tích.
Đối với chu vi, chúng ta chỉ cần tính tổng độ dài các cạnh xung quanh của hình thoi.
5. Lưu ý khi tính diện tích, chu vi hình thoi
– Khi tính diện tích hình thoi, chúng ta cần lưu ý đơn vị của diện tích là đơn vị chiều dài + vuông như cm2, m2,…
– Chúng ta cần đảm bảo rằng đơn vị đo chiều dài của hai đường chéo, cạnh và chiều cao là cùng một đơn vị trước khi tính toán.
Công Thức Tính Đường Chéo Hình Thoi
Dựa vào các công thức tính chu vi hình thoi, diện tích hình thoi ở trên, chúng ta cũng có thể dễ dàng tìm được công thức tính đường chéo hình thoi như sau:
* Tính đường chéo hình thoi khi biết diện tích, độ dài 1 đường chéo: Nếu đã biết diện tích hình thoi, độ dài đường chéo (d1), chúng ta sẽ dễ dàng tìm được 1 cạnh còn lại của hình thoi theo công thức sau: d2 = 2S/ d1
6. Bài tập tính diện tích hình thoi
Xem thêm : ✅ Công thức axit axetic ⭐️⭐️⭐️⭐️⭐
Bài 1: Cho hình thoi ABCD có cạnh AD = 4m, có góc DAB = 30 độ. Tính diện tích của hình thoi ABCD.
Giải:
Do ABCD là hình thoi nên các tam giác tạo thành là tam giác cân, gọi I là trung điểm hai đường chéo nên AI vuông góc với BD, góc IAB = 15 độ.Do đó, AI = AB. cos IAB = 4. Cos 15 = 3,84m.Xét tam giác vuông ABI, theo định lý Pytago, ta có:BI2 = AB2- AI2 = 1,25 m.Nên BI = 1,1m
+ AC = 2. AI = 7,68 m.
+ BD = 2. BI = 2,2 m.
Do đó, diện tích của hình thoi ABCD = ½ . AC . BD = 8,45 (m2)
Bài Tập Liên Quan Tới Diện Tích, Chu Vi Hình Thoi
Bài 2: Tính diện tích hình thoi ABCD, khi biết cạnh AB = 5cm, đường chéo AC = 8cm.
Giải:
Gọi I là giao điểm của AC và BD, ta có AI = IC = 4cmXét tam giác vuông ABI, ta có:BI2 = AB2- AI2Thay AI = 4cm, AB = 5cm, ta được: BI = 3cmMà BD = 2.BI = 2.3 = 6cmDiện tích hình thoi ABCD: S = (BD . AC) : 2 = 24(cm2)
Bài 3: Cho hình thoi ABCD có chu vi bằng 20cm, đường chéo BD = 6cm. Tính độ dài đường chéo AC.
Giải:
Gọi I là giao điểm của AC và BD. Xét tam giác vuông IAB có AI2 + AB2 = IB2. Thay AI = AB = 6 và IB = 3. Do đó, diện tích của hình thoi ABCD là: S = 1/2 x AC x BD = 20cm2
Bài 4: Tính diện tích của hình thoi ABCD, biết: BD = 9m, AC = 15m
Giải:
Diện tích của hình thoi ABCD là: S = 1/2 x AC x BD = 67.5 m2
Bài 5: Một hình thoi có diện tích 4dm2, độ dài một đường chéo là 5dm. Tính độ dài đường chéo thứ hai.
Giải:
Độ dài đường chéo thứ hai là: 2 x diện tích / độ dài đường chéo 1 = 2 x 4 / 5 = 1.6 dm
Bài 6: Một khu đất hình thoi có độ dài đường chéo là 70m và 300m. Tính diện tích của khu đất đó.
Giải:
Diện tích khu đất là: 1/2 x AC x BD = 10500 m2
Các ví dụ khác về tính diện tích và chu vi hình thoi
Trên đây là một số ví dụ về tính diện tích và chu vi hình thoi.
Nguồn: https://vatlytuoitre.com
Danh mục: Định luật
